1. Introduction▲
En programmation orientée objet, un décorateur est un « patron de conception » (design pattern) qui permet notamment d'ajouter statiquement (à la compilation) ou dynamiquement (à l'exécution) des responsabilités à un objet individuel, sans modifier la classe à laquelle appartient l'objet ni les autres instances de cette classe.
Cette notion a été élargie à d'autres modèles de programmation. Par exemple, la PEP 318 de Python introduit la notion de décorateurs, qui sont des fonctions permettant de modifier le comportement d'autres fonctions sans en modifier le code source (voir l'article Concepts Python avancés - Les décorateurs, d'Alexandre Galodé, sur ce site).
Les décorateurs sont utiles pour modifier le comportement de fonctions complexes ou héritées que vous ne voulez pas toucher, par exemple parce qu'elles figurent dans un module qu'il est souhaitable de laisser intact.
Perl n'a pas de syntaxe intégrée spécifique pour créer ou utiliser des décorateurs, mais nous verrons qu'il est possible d'utiliser des fonctions d'ordre supérieur et des typeglob pour combler aisément cette lacune.
2. Pourquoi décorer une fonction ?▲
2-1. Afficher une trace des appels à une fonction▲
Considérons une fonction importante ou complexe dont nous souhaitons tracer les appels ou en décompter le nombre. Notre première fonction, très simple, affiche la réponse à la grande question sur la vie, l'univers et le reste :
use strict;
use warnings;
use feature 'say';
affiche_la_reponse();
sub affiche_la_reponse {
say "42";
}Si nous désirons créer une fonction wrapper qui trace les appels à la fonction affiche_la_reponse, sans en modifier le code, nous pourrions écrire une fonction trace_appels imprimant les informations voulues et appelant ensuite affiche_la_reponse :
my $count = 0;
sub trace_appels {
$count++;
say "Appel numéro $count de la fonction surveillée";
affiche_la_reponse();
}
trace_appels() for 1..3;Ceci va bien afficher les trois appels de fonction :
$ perl trace_appels.pl
Appel numéro 1 de la fonction surveillée
42
Appel numéro 2 de la fonction surveillée
42
Appel numéro 3 de la fonction surveillée
42Mais cela n'est pas très satisfaisant. Si nous désirons surveiller les appels d'une autre fonction, nous devons écrire une nouvelle version de trace_appels, avec l'appel de l'autre fonction. Nous voudrions donc une fonction générique qui puisse tracer les appels d'une fonction quelconque. Il est par conséquent souhaitable de passer en paramètre la fonction à surveiller. C'est ce que fait la fonction enrichit ci-dessous :
my $count = 0;
sub enrichit {
my $fonction = shift;
$count++;
say "Appel numéro $count de la fonction surveillée";
$fonction->();
}
enrichit(\&affiche_la_reponse) for 1..3;L'argument \&affiche_la_reponse passé à la fonction enrichit est une référence à la fonction affiche_la_reponse, c'est-à-dire une variable scalaire contenant l'adresse de la fonction appelée. On appelle souvent ce genre de variable une coderef (une référence à du code). Et une fonction ainsi passée en paramètre à une autre fonction pour y être éventuellement appelée est généralement nommée fonction de rappel (callback function). Ce mécanisme est décrit plus en détail dans le chapitre Les références vers des fonctions de la deuxième partie de mon tutoriel sur la programmation fonctionnelle en Perl.
Quand une fonction peut être passée en paramètre à une autre fonction, ou être renvoyée comme valeur de retour d'une autre fonction, on parle souvent de fonctions d'ordre supérieur. On dit parfois aussi que les fonctions sont des citoyennes de première classe.
Dans la fonction enrichit, le code récupère l'argument passé (la coderef), incrémente le compteur (comme précédemment), affiche la trace et appelle la coderef reçue en paramètre avec la syntaxe $fonction->(). Même si la syntaxe est nouvelle pour vous, cela n'a rien de bien mystérieux : la fonction enrichit reçoit en paramètre une référence vers une fonction et appelle cette fonction.
Ce programme affiche la même chose que précédemment, mais nous avons maintenant une fonction décoratrice générique qui peut prendre une autre fonction qu'affiche_la_reponse en paramètre :
sub hello_world {
say "Hello world";
}
# ... même définition de la fonction enrichit que précédemment
enrichit(\&hello_world) for 1..3;Ce qui affiche :
$ perl enrichit.pl
Appel numéro 1 de la fonction surveillée
Hello world
Appel numéro 2 de la fonction surveillée
Hello world
Appel numéro 3 de la fonction surveillée
Hello worldÀ vrai dire, notre fonction enrichit est encore un peu squelettique et ne permet en particulier pas le passage de paramètres à la fonction surveillée (puisque nous n'en avions pas besoin dans nos deux exemples). Il n'est guère difficile d'ajouter cette fonctionnalité :
sub enrichit {
my $fonction = shift;
$count++;
say "Appel numéro $count de la fonction surveillée";
$fonction->(@_);
}
enrichit(\&fonction_surveillee, $param1, $param2);Maintenant, le premier paramètre passé à enrichit est dépilé du tableau @_ par l'appel à la fonction shift, et les autres paramètres sont passés à la fonction surveillée.
Nous avons donc bien progressé, puisque nous pouvons maintenant tracer les appels d'une fonction quelconque, mais nous n'avons pas réellement modifié le comportement de la fonction à tracer, nous avons seulement fait en sorte d'encapsuler son appel dans du code se chargeant d'afficher les traces d'appel.
Surtout, nous devons pour l'instant appeler la fonction surveillante (enrichit) chaque fois que nous voulons tracer les appels de la fonction surveillée (affiche_la_reponse), alors que nous aimerions modifier le comportement de la fonction surveillée. En effet, si la fonction surveillée est appelée à de multiples endroits dans le code, nous devons pour l'instant modifier chaque appel de cette fonction, ce qui n'est pas pleinement satisfaisant. J'avais initialement appelé decorateur la fonction enrichit, mais j'ai préféré abandonner ce premier nom pour l'instant, car nous ne sommes pas encore en présence d'un vrai décorateur. Nous verrons plus loin dans ce tutoriel (section 3.4) comment modifier réellement le comportement de la fonction surveillée, mais nous allons d'abord examiner un autre exemple dans lequel nous pourrions désirer enrichir dynamiquement une fonction existante.
2-2. La suite de Fibonacci▲
Considérons une fonction de calcul de la suite de Fibonacci. Une suite de Fibonacci est une suite de nombres telle que chaque nombre est la somme des deux nombres qui le précèdent, par exemple : 1, 1, 2, 3, 5, 8, 13, 21... (Selon les définitions, les deux premiers nombres sont généralement soit 1 et 1, soit 0 et 1 ; mais on pourrait très bien définir une telle suite avec 4 et 7 comme premiers nombres, ce qui donnerait la suite 4, 7, 11, 18….)
En notation mathématique, on peut décrire la suite de Fibonacci comme suit :
F1 = 1, F2 = 1, et Fn = Fn-1 + Fn-2
2-2-1. Mise en œuvre récursive▲
Nous pouvons mettre en place la fonction récursive suivante :
2-2-2. Problème de performance▲
C'est simple, ça marche, mais cela pose un problème : cette fonction devient très lente, voire très très lente, avec des paramètres en entrée plus élevés.
Modifions la dernière ligne afin de passer le nombre de Fibonacci à calculer en paramètre au programme :
say fibo shift;et appelons notre programme avec la fonction time d'Unix ou de Linux pour mesurer le temps de calcul pour les valeurs 20, 30 et 40 :
$ time perl fibo.pl 20
6765
real 0m0.073s
user 0m0.000s
sys 0m0.030s
$ time perl fibo.pl 30
832040
real 0m1.151s
user 0m1.093s
sys 0m0.000s
$ time perl fibo.pl 40
102334155
real 2m6.626s
user 2m6.328s
sys 0m0.030sOn a donc les durées d'exécution suivantes :
- moins d'un dixième de seconde pour la valeur 20,
- 1,15 seconde pour la valeur 30, et
- plus de deux minutes pour la valeur 40.
N'essayez pas de calculer le cinquantième et encore moins centième nombre de Fibonacci avec ce programme : pour le centième nombre de Fibonacci, il faudrait une durée d'exécution d'environ 13,8 millions d'années (encore que le programme planterait sans doute bien avant pour mémoire insuffisante). Pour le 115e nombre de Fibonacci, la durée d'exécution prévisionnelle (18,9 milliards d'années) dépasserait l'âge actuel de l'univers. Nous avons ici ce qu'on appelle communément une explosion exponentielle.
2-2-3. Pourquoi cette explosion exponentielle ?▲
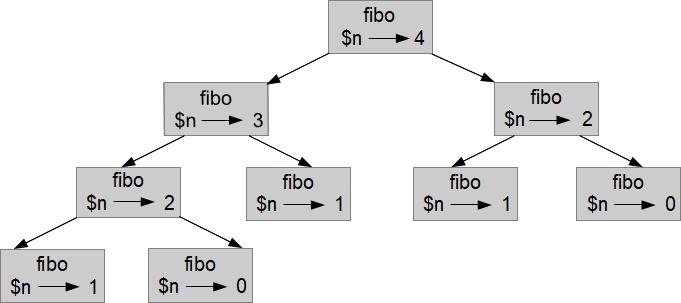
Pour comprendre pourquoi cette fonction devient aussi lente quand le nombre de Fibonacci à calculer croît (même modérément), considérons l'arbre d'appels du programme avec n = 4 :
Pour n = 4, la fonction fibo appelle deux fois la fonction fibo avec les valeurs 3 et 2. Pour n = 2, fibo est encore appelée deux fois. Pour n = 3, on appelle encore deux fois fibo, avec les valeurs 1 et 2. Et pour n = 2, la fonction est encore appelée deux fois. Au total, la fonction est appelée neuf fois, deux fois avec la valeur 0, trois fois avec la valeur 1, deux fois avec la valeur 2, et une fois pour les valeurs 3 et 4. Donc, on recalcule plusieurs fois la même chose, ce qui n'est pas très efficace. Plus on recherche un nombre de Fibonacci élevé, plus le nombre de calculs inutiles augmente, et il augmente très rapidement.
Considérons le nombre total d'appels de la fonction fibo pour les premiers nombres de Fibonacci :
|
Nombre de Fibonacci à calculer |
Utilise fibo(n-1) |
Utilise fibo(n-2) |
Nombre total d'appels de fibo :
|
Rapport avec le nombre d'appels précédent |
|---|---|---|---|---|
|
0 |
- |
- |
1 |
|
|
1 |
- |
- |
1 |
1 |
|
2 |
1 |
0 |
3 |
3 |
|
3 |
2 |
1 |
5 |
1,66666667 |
|
4 |
3 |
2 |
9 |
1,80000000 |
|
5 |
4 |
3 |
15 |
1,66666667 |
|
6 |
5 |
4 |
25 |
1,6666667 |
|
… |
… |
… |
... |
|
|
28 |
27 |
26 |
1028457 |
1,61803493 |
|
29 |
28 |
27 |
1664079 |
1,61803459 |
|
30 |
29 |
287 |
2692537 |
1,61803436 |
|
… |
… |
… |
… |
... |
|
50 |
49 |
48 |
40730022147 |
1,61803399 |
Si l'on divise le nombre d'appels pour fibo(29) par celui pour fibo(28), on obtient 1,61803459 (colonne de droite dans le tableau ci-dessus). Entre fibo(30) et fibo(29) le rapport est 1,61803436. On constate qu'à chaque étape, le nombre d'appels de la fonction fibo est multiplié par environ 1,618 (du moins dès que l'on s'éloigne des très petits nombres). On est donc en présence d'une progression géométrique (approximative au début) dont la raison est assez rapidement de l'ordre de 1,61803.
Le rapport entre deux nombres successifs d'appels converge assez vite vers le nombre 1,6180339887499, qui se trouve être ce que l'on appelle généralement le nombre d'or. Au sujet du nombre d'or et de ses relations avec la suite de Fibonacci, voir l'Annexe : le nombre d'or (ou divine proportion) à la fin de ce document.
2-2-4. Corriger ce problème de performance▲
Le programme est très lent pour des valeurs un peu élevées en entrée parce que la fonction fibo est appelée un nombre considérable de fois :
- fibo(10) : 177 fois
- fibo (20) : 21 891 fois (123 fois plus que fibo (10))
- fibo (30) : 2 692 537 fois
- fibo (40) : 331 160 281 fois (15127 fois plus que fibo (20))
- fibo (100) : plus de mille milliards de milliards de fois (environ 1,14 x 1021).
Pour le calcul de fibo(10), la fonction fibo est appelée 10 fois pour calculer une valeur nouvelle, et 167 fois pour recalculer des valeurs déjà calculées antérieurement. De même, pour le calcul de fibo(30), la fonction fibo est appelée 30 fois pour calculer une nouvelle valeur et 2 692 507 fois inutilement.
Si l'on stocke et réutilise les valeurs déjà calculées, on peut éliminer ces innombrables appels inutiles à la fonction fibo. Stocker une valeur déjà obtenue pour éviter de devoir la recalculer s'appelle la cacher et l'endroit où l'on stocke ces valeurs s'appelle un cache (ou parfois un mémo). On dit parfois que l'on échange de l'espace mémoire contre du temps de calcul CPU. Il suffit donc de stocker dans un hachage (ou même un simple tableau dans ce cas) les valeurs que l'on calcule et de ne rappeler la fonction fibo que quand la valeur n'est pas encore connue.
Modifions donc notre programme pour ajouter la gestion d'un cache :
use strict;
use warnings;
use feature 'say';
my @cache = qw /0 1/; # deux valeurs de départ pour fibo(0) et fibo(1)
sub fibo {
my $n = shift;
$cache[$n] = fibo($n-1) + fibo($n-2) unless defined $cache[$n];
return $cache[$n];
}
say fibo shift;En initialisant le cache pour les deux premiers nombres de Fibonacci, nous n'avons plus besoin de traiter à part les cas pour lesquels $n est inférieur à 2 (ce qui servait à arrêter la récursion) et le code est plus court que celui de notre première version.
La fonction fibo n'est plus appelée que le nombre de fois où cet appel est vraiment nécessaire et nous éliminons tous les appels inutiles. L'exécution est maintenant presque instantanée et ne paraît même plus dépendre vraiment de la taille du nombre de Fibonacci recherché :
$ time perl fibo.pl 10
55
real 0m0.057s
user 0m0.000s
sys 0m0.015s
$ time perl fibo.pl 20
6765
real 0m0.063s
user 0m0.000s
sys 0m0.015s
$ time perl fibo.pl 90
2880067194370816120
real 0m0.065s
user 0m0.000s
sys 0m0.015sLe problème de performance est donc résolu, mais nous avons dû modifier le code de la fonction fibo, ce qui n'est pas le but dans ce document : nous désirons modifier son comportement sans en modifier le code. Les décorateurs nous permettront d'y parvenir.
3. Un premier décorateur : tracer les appels de fonctions▲
Un décorateur est une fonction d'ordre supérieur qui prend une fonction en argument et en renvoie une nouvelle avec un comportement modifié. Commençons par traiter le premier cas que nous avions examiné ci-dessus, un exemple simple qui se contente d'ajouter une impression de débogage avant et après l'appel de la fonction.
3-1. Créer la fonction décoratrice▲
Le code du décorateur lui-même pour ajouter des traces de débogage ressemblerait à ceci :
use strict;
use warnings;
use feature 'say';
sub triplement {
return 3 * shift;
}
my $triplement_decore = decorateur(\&triplement);
say $triplement_decore->($_) for 10, 15, 20;
sub decorateur {
my $coderef = shift;
return sub {
say "Appel de la fonction avec les arguments: @_";
my $resultat = $coderef->(@_);
say "Valeur de retour: $resultat.";
return $resultat;
}
}La fonction decorateur prend en entrée une référence à une fonction (ici, la fonction triplement) et renvoie une nouvelle fonction qui utilise la fonction d'origine, mais ajoute de nouvelles fonctionnalités « autour d'elle » (avant et après son appel).
Si vous désirez de plus amples informations sur les fonctions retournant des fonctions, vous pouvez consulter le chapitre sur les Usines à fonction de la deuxième partie de mon tutoriel sur la programmation fonctionnelle en Perl.
À l'exécution, cela donne :
$ perl decorateur.pl
Appel de la fonction avec les arguments: 10
Valeur de retour: 30.
30
Appel de la fonction avec les arguments: 15
Valeur de retour: 45.
45
Appel de la fonction avec les arguments: 20
Valeur de retour: 60.
60Nous avons maintenant avec $triplement_decore une référence vers une fonction anonyme qui assure à la fois les tâches de la fonction triplement de départ et celles de traçage des appels.
3-2. Enrichir le décorateur▲
Nous pouvons enrichir notre fonction decorateur pour numéroter les appels :
sub decorateur {
my $coderef = shift;
my $num_appel = 1;
return sub {
say "Appel numéro $num_appel de la fonction avec les arguments: @_";
$num_appel++;
my $resultat = $coderef->(@_);
say "Valeur de retour: $resultat.";
return $resultat;
}
}Par rapport à la précédente version, nous avons ajouté la déclaration et l'initialisation d'un compteur, $num_appel, dans le code de préparation de decorateur, et ajouté l'utilisation de ce compteur et son incrémentation dans la fonction anonyme renvoyée par le décorateur. Cette fonction anonyme devient ce que l'on appelle une fermeture (closure). Lorsqu'une fonction anonyme est définie de cette façon, elle garde la trace des variables qui existaient lors de sa définition (si ces variables sont utilisées dans le corps de ladite fonction anonyme). C'est ce qui permet à la variable num_appel de conserver sa valeur d'un appel de la fonction anonyme au suivant. Pour plus d'informations à ce sujet, voir le chapitre sur les fermetures de mon tutoriel susmentionné.
À l'exécution, on obtient les traces enrichies suivantes :
$ perl decorateur.pl
Appel numéro 1 de la fonction avec les arguments: 10
Valeur de retour: 30.
30
Appel numéro 2 de la fonction avec les arguments: 15
Valeur de retour: 45.
45
Appel numéro 3 de la fonction avec les arguments: 20
Valeur de retour: 60.
603-3. Décorateur en contexte scalaire ou de liste?▲
Le décorateur vu précédemment supposait que la fonction à décorer renvoyait une valeur scalaire. Il est facile de l'adapter pour une fonction comme multiplie234 renvoyant une liste :
sub multiplie234 {
return $_[0] * 2, $_[0] * 3, $_[0] * 4;
}
my $multiplie_decore = decorateur(\&multiplie234);
say $_ for $multiplie_decore->(20);
sub decorateur {
my $coderef = shift;
my $num_appel = 1;
return sub {
say "Appel numéro $num_appel de la fonction avec les arguments: @_";
$num_appel++;
my @resultat = $coderef->(@_);
say "Valeurs de retour: @resultat.";
return @resultat;
}
}Ce qui affiche :
$ perl decorateur.pl
Appel numéro 1 de la fonction avec les arguments: 20
Valeurs de retour: 40 60 80.
40
60
80Cette nouvelle version de decorateur fonctionne à la fois en contexte scalaire et de liste et nous permet de décorer aussi bien la fonction multiplie234 que la fonction triplement :
my $multiplie_decore = decorateur(\&multiplie234);
say $_ for $multiplie_decore->(20);
my $triplement_decore = decorateur(\&triplement);
say $triplement_decore->($_) for 5, 10, 15;Ce qui affiche :
Appel numéro 1 de la fonction avec les arguments: 20
Valeur de retour: 40 60 80.
40
60
80
Appel numéro 1 de la fonction avec les arguments: 5
Valeur de retour: 15.
15
Appel numéro 2 de la fonction avec les arguments: 10
Valeur de retour: 30.
30
Appel numéro 3 de la fonction avec les arguments: 15
Valeur de retour: 45.
45Dans la pratique, concevoir des décorateurs qui renvoient des listes de résultats et non de simples valeurs scalaires est souvent plus souple. Mais ce n'est pas une règle absolue : dans certains cas, on aura besoin de plusieurs décorateurs pour faire face aux différentes situations. C'est donc une décision de conception qui devra être prise par le développeur.
3-4. Remplacer la fonction d'origine par sa version décorée▲
Nous avons un peu retardé ce moment légèrement délicat, mais il faut bien y venir. Jusqu'à maintenant, toutes nos fonctions d'enrichissement ou de décoration créaient une autre fonction apportant de nouvelles fonctionnalités, mais ne remplaçaient pas vraiment la fonction d'origine.
Un vrai décorateur doit modifier le comportement de la fonction d'origine, et nous arrivons à cette étape essentielle de notre projet.
3-4-1. Et hop, un petit tour de magie blanche▲
Nous allons devoir recourir à un petit tour de magie relevant des fonctionnalités relativement avancées de Perl, mais c'est cependant très simple. Perl nous permet de modifier la table des symboles du paquetage courant, ce qui nous permet de remplacer la fonction d'origine par la fonction nouvellement créée.
Dans notre programme, remplaçons les lignes de code suivantes :
my $triplement_decore = decorateur(\&triplement);
say $triplement_decore->($_) for 10, 15, 20;par celles-ci :
*main::triplement = decorateur(\&triplement);
say triplement($_) for 10, 15;et nous obtenons la sortie suivante :
$ perl decorateur.pl
Subroutine main::triplement redefined at decorateur.pl line 10.
Appel numéro 1 de la fonction avec les arguments: 10
Valeur de retour: 30.
30
Appel numéro 2 de la fonction avec les arguments: 15
Valeur de retour: 45.
45Maintenant, nous obtenons l'affichage recherché (à part le warning que nous traiterons plus loin) en appelant simplement la fonction triplement. Nous avons bien modifié le comportement de triplement sans en changer le code. *main::triplement est un typeglob, qui nous permet d'accéder à la table des symboles de Perl, c'est-à-dire la structure de données contenant notamment les variables « globales » (de paquetage) et les noms des fonctions.
La table des symboles
La table des symboles est une structure de données (une espèce de hachage un peu particulière) contenant les identifiants d'un programme : variables « globales » (de paquetage), les noms des fonctions, des formats et des descripteurs de fichiers (filehandles) et de répertoires non lexicaux, etc. Les variables lexicales (définies avec le mot-clef my) ne figurent pas dans la table des symboles. Il existe une table des symboles pour chaque paquetage (souvent un module) déclaré dans un programme et une table pour le programme principal, nommée %main::. On peut consulter son contenu avec le petit script uniligne suivant :
# Remplacer les apostrophes par des guillemets sous Windows
$ perl -E 'say for keys %main::'En examinant le contenu affiché, on reconnaîtra notamment ARGV, ENV, _, qui sont le nom des variables spéciales @ARGV, %ENV, $_ et @_, mais sans le sigil initial. Chaque identifiant peut donc représenter plusieurs variables ayant le même identifiant, mais des sigils différents :
$ perl -E '$toto = 1; @toto = (2, 3);
> say $main::toto; say "@main::toto"; '
1
2 3Pour qu'un identifiant puisse représenter plusieurs variables différentes, chaque élément de la table des symboles est lui-même une référence sur une espèce de hachage (appelé stash). On accède à un élément de la table des symboles avec la syntaxe de typeglob *identifiant, et à ses composantes avec une syntaxe de hachage utilisant les clefs SCALAR, ARRAY, CODE, HASH, etc. :
$ perl -E '$toto = 1; @toto = (2, 3);
> $titi = *toto{SCALAR}; say $$titi;
> $tata = *toto{ARRAY}; say "@$tata";'
1
2 3On ne peut pas attribuer une valeur en utilisant *toto{SCALAR} à gauche de l'affectation, mais on peut créer un alias entre deux typeglobs :
$ perl -E '$toto = "scalaire"; @toto = 1..5;
> *titi = *toto; say $titi; say "@titi";'
scalaire
1 2 3 4 5On n'est pas obligé d'affecter l'ensemble d'un typeglob. Dans le code ci-dessous, je redéfinis *titi en lui affectant une référence au scalaire $tata. Cela redéfinit la valeur de $titi (et de $toto) sans affecter la variable @titi :
$ perl -E '$toto = "scalaire"; @toto = 1..5; $tata = 5;
> *titi = *toto; *titi = \$tata;
> say $titi; say "@titi"; say $toto;'
5
1 2 3 4 5
5Si vous utilisez le pragma use strict; avec le code ci-dessus (et vous devriez vraiment le faire pour tout script de plus d'une ligne), il vous faudra prédéclarer les variables globales $titi et @titi avec le mot-clef our :
$ perl -E 'use strict; our $toto = 42; our @toto = 1..5;
> my $tata = 5; our ($titi, @titi);
> *titi = *toto; *titi = \$tata;
> say $titi; say "@titi"; say $toto;'
5
1 2 3 4 5
5ou à la rigueur désactiver localement strict pour les variables (avec l'instruction no strict 'vars';) lors de leur utilisation :
$ perl -Mstrict -E ' our $toto = 42; our @toto = 1..5;
> my $tata = 5; *titi = *toto; *titi = \$tata;
> { no strict "vars"; say $titi; say "@titi"; }
> say $toto;'
5
1 2 3 4 5
5Nous pouvons réaliser le même type d'affectation avec des fonctions. Dans le code ci-dessous, nous définissons une fonction square puis créons un alias francophone, carre, pour cette fonction :
$ perl -Mstrict -E 'sub square {
> my $arg = shift; return $arg * $arg;
> }
> *carre = *square;
> say carre(10); '
100C'est cette fonctionnalité que nous utilisons dans le présent document pour mettre en place nos fonctions décorées.
En affectant la valeur de retour de décorateur à *main::triplement, nous redéfinissons la fonction triplement dans cette table des symboles, si bien qu'un appel à cette fonction conduit désormais à l'appel de la version décorée de cette fonction. Ici, nous aurions aussi pu utiliser le typeglob *::triplement, qui accède également à la table des symboles du paquetage courant, mais il peut être préférable (notamment pour la suite) de spécifier que nous voulons modifier la table des symboles du paquetage principal.
Cela fonctionne, mais il reste au moins deux petits problèmes à résoudre : un avertissement intempestif sur la redéfinition de la fonction triplement, et une syntaxe quelque peu rébarbative.
3-4-2. Suppression de l'avertissement de redéfinition▲
Pour ce qui est du warning sur la redéfinition de la fonction :
Subroutine main::triplement redefined at decorateur.pl line 10nous pourrions désactiver les warnings en général, mais ce n'est pas souhaitable : nous désirons continuer à bénéficier des warnings, qui nous prémunissent contre bon nombre d'erreurs de codage. Il suffit de dire à Perl d'accepter sans mot dire ce genre de redéfinition (et ne supprimer aucun autre warning). Comme il est de bonne politique de réduire au maximum la portée lexicale d'une telle instruction de désactivation des warnings, nous la mettrons dans un bloc avec l'instruction d'affectation, ce qui donne par exemple :
{
no warnings 'redefine';
*main::triplement = decorateur(\&triplement);
}
say triplement($_) for 15, 30;Ceci permet de supprimer uniquement ce warning (en gardant les autres), et de ne le faire que pour la seule ligne de code concernée.
Maintenant, nous n'avons plus cet avertissement :
$ perl decorateur.pl
Appel numéro 1 de la fonction avec les arguments: 15
Valeur de retour: 45.
45
Appel numéro 2 de la fonction avec les arguments: 30
Valeur de retour: 90.
903-4-3. La table des symboles d'un module particulier▲
Considérons le module Multiplie.pm très simple suivant :
#!/usr/bin/perl
package Multiplie;
use strict;
use warnings;
require Exporter;
our @ISA = qw/Exporter/;
our @EXPORT = qw (quadruplement);
sub quadruplement {
return 4 * shift;
};
# ... autres fonctions éventuelles
1;Ce module exporte la fonction quadruplement qui renvoie son argument multiplié par quatre.
Il pourra être utilisé par le programme suivant :
#!/usr/bin/perl
use strict;
use warnings;
use feature 'say';
use Multiplie;
say quadruplement($_) for 5, 15;Si nous désirons enrichir la fonction quadruplement, nous pouvons le faire au sein du module, en utilisant le nom du module :
{
no warnings 'redefine';
*{Multiplie::quadruplement} = decorateur(\&quadruplement);
}
sub quadruplement {
return 4 * shift;
};
sub decorateur {
my $coderef = shift;
my $num_appel = 1;
return sub {
say "Appel n° $num_appel de la fonction avec les arguments: @_";
$num_appel++;
my $resultat = $coderef->(@_);
say "Valeur de retour: $resultat.";
return $resultat;
}
}Cela fonctionne bien et affiche :
$ perl quadruple.pl
Appel n° 1 de la fonction avec les arguments: 5
Valeur de retour: 20.
20
Appel n° 2 de la fonction avec les arguments: 15
Valeur de retour: 60.
60Il est également possible d'utiliser la variable spéciale __PACKAGE__ lors de la redéfinition de la fonction (moyennant un hack un peu discutable, mais c'est pour la bonne cause) :
{
no warnings 'redefine';
no strict 'refs';
*{__PACKAGE__ . "::quadruplement"} = decorateur(\&quadruplement);
}Cela oblige à utiliser une référence symbolique (et donc le pragma no strict 'refs';), ce qui ne me satisfait pas entièrement (mais je n'ai pas trouvé d'autre moyen). De toute façon, cela ne semble pas apporter grand-chose : on sait que l'on est dans un module, on peut aussi bien utiliser son nom codé en dur, on ne gagne guère de généricité ici. Cela ne semble avoir de l'intérêt que si notre module est appelé par plusieurs autres modules. Dans le cas le plus fréquent, il semble plus intéressant de faire la modification au niveau du programme principal appelant.
En fait, l'un des cas les plus courants où l'on désire décorer une fonction est celui où il faudrait modifier le comportement d'une fonction se trouvant dans un module public (module standard ou du CPAN, par exemple). Modifier le code d'un module n'est généralement pas souhaitable, car c'est s'exposer à toutes sortes de problèmes dans l'avenir, en particulier à l'occasion de mises à jour. Il est bien préférable de laisser le module en l'état et d'utiliser un décorateur pour modifier le comportement sans toucher le code.
Décorer la fonction d'un module au sein du programme principal est très simple. On garde le module inchangé et le programme principal appelant est modifié comme suit :
{
no warnings 'redefine';
*main::quadruplement = decorateur(\&quadruplement);
}
say quadruplement($_) for 5, 15;
sub decorateur {
my $coderef = shift;
my $num_appel = 1;
return sub {
say "Appel numéro $num_appel de la fonction avec les arguments: @_";
$num_appel++;
my $resultat = $coderef->(@_);
say "Valeur de retour: $resultat.";
return $resultat;
}
}La version décorée de notre fonction s'installe cette fois dans la table des symboles principale. Et tout marche comme précédemment.
3-5. Automatiser l'installation du décorateur▲
Tout le monde n'aime pas manipuler directement la table des symboles (moi le premier).
On peut créer une fonction decore pour s'en occuper à notre place :
sub decore {
my ($sub_name, $decorator) = @_;
no warnings 'redefine';
no strict 'refs';
*{"main::$sub_name"} = $decorator->(\&{$sub_name});
}
# la mise en place de la décoration est maintenant très simple:
decore ("triplement", \&decorateur);
say triplement($_) for 15, 30;Cela marche comme précédemment et affiche le même type de résultat.
Vous pouvez maintenant mettre la fonction decore dans un module permettant d'exporter cette fonction et oublier les menues entorses aux règles usuelles de bonne pratique qu'elle se permet exceptionnellement de faire. Il existe de nombreux modules faisant ce genre de choses et que vous utilisez probablement assez régulièrement.
Rappelez-vous seulement qu'il faut lui passer le nom de la fonction à décorer (sous la forme d'une chaîne de caractères) et une référence vers le décorateur.
4. Retour à la fonction de Fibonacci▲
Revenons à la version initiale de la fonction fibo calculant récursivement les nombres de Fibonacci (voir section 2.2.1). Cette fonction avait la forme suivante :
sub fibo {
my $n = shift;
if ($n < 2) {
return $n;
} else {
return fibo ($n-1) + fibo ($n-2);
}
}Cette fonction présentait l'inconvénient de devenir extrêmement lente pour des nombres de Fibonacci un peu élevés, et nous avions réécrit la fonction avec l'utilisation d'un cache pour éviter de recalculer de nombreuses fois des valeurs déjà connues et obtenir des performances incomparablement meilleures.
4-1. Décorer la fonction de calcul des nombres de Fibonacci ▲
Nous pouvons maintenant laisser la fonction d'origine intacte et utiliser un décorateur pour effectuer la mise en cache des valeurs connues. Appelons cache notre décorateur :
sub cache {
my $code_ref = shift;
my @memo = (0, 1);
return sub {
my $n = shift;
$memo[$n] = $code_ref->($n) unless defined $memo[$n];
return $memo[$n];
}
}La fonction fibo d'origine (référée par $code_ref) n'est appelée que si le nombre en entrée n'est pas défini dans le tableau @memo.
Nous pouvons maintenant installer la fonction décorée à l'aide de decore et l'appeler :
decore("fibo", \&cache);
say fibo(shift);Et les durées d'exécution sont tout à fait satisfaisantes :
$ time perl fibo_decoree.pl 10
55
real 0m0.214s
user 0m0.015s
sys 0m0.015s
$ time perl fibo_decoree.pl 20
6765
real 0m0.191s
user 0m0.015s
sys 0m0.015s
$ time perl fibo_decoree.pl 30
832040
real 0m0.241s
user 0m0.015s
sys 0m0.046s
$ time perl fibo_decoree.pl 40
102334155
real 0m0.202s
user 0m0.000s
sys 0m0.046s
$ time perl fibo_decoree.pl 90
2880067194370816120
real 0m0.250s
user 0m0.031s
sys 0m0.046sLes durées d'exécution sont un peu plus longues que pour la version avec le cache codé en dur de la section 2.2.4, mais cela est dû au fait que l'instruction time du shell mesure aussi la durée de compilation du programme, qui est plus longue avec l'utilisation du décorateur (cache) et l'importation de la fonction decore de notre module externe. Nous pouvons calculer presque instantanément un nombre de Fibonacci assez grand.
4-2. Le module memoize▲
Ajouter un cache à une fonction est une opération suffisamment courante pour qu'il vaille la peine de l'automatiser pleinement et de la rendre générique. Modifions d'abord légèrement le décorateur cache :
sub cache {
my $code_ref = shift;
my %memo;
return sub {
my $n = shift;
$memo{$n} = $code_ref->($n) unless defined $memo{$n};
return $memo{$n};
}
}Par rapport à la version précédente, nous avons utilisé un hachage (%memo) au lieu d'un tableau pour le cache. Un tableau suffisait pour les nombres de Fibonacci parce nous utilisions en entrée des entiers positifs consécutifs. Utiliser un hachage permet l'utilisation de clefs bien plus générales que des entiers consécutifs.
Avec la fonction fibo, cela fonctionne comme précédemment. Mais nous pouvons maintenant ajouter un cache à une autre fonction, selon nos besoins, même si les données en entrée sont des chaînes de caractères ou des nombres quelconques.
Ajouter un cache à une fonction n'est pas très difficile. Les changements à faire sont essentiellement les mêmes pour toute fonction. La transformation automatique d'une fonction pour lui ajouter un cache s'appelle la mémoïsation (on parle bien de mémoïsation, et non de mémorisation, rappelez-vous que le terme mémo est à peu près synonyme de cache), et la fonction ainsi modifiée est mémoïsée. Le décorateur cache de la section précédente, associé à la fonction decore, assure la mémoïsation de la fonction qui lui est passée en paramètre.
Nous pouvons écrire une fonction memoize qui se charge entièrement de cette mémoïsation automatique :
use strict;
use warnings;
use feature 'say';
sub fibo {
my $n = shift;
return $n if $n < 2;
return fibo ($n-1) + fibo ($n-2);
}
sub memoize {
my $sub_name = shift;
my %memo;
my $code_ref = \&{$sub_name};
my $new_func = sub {
my $n = shift;
$memo{$n} = $code_ref->($n) unless defined $memo{$n};
return $memo{$n};
};
no warnings 'redefine';
no strict 'refs';
*{"main::$sub_name"} = $new_func;
}
memoize("fibo");
say fibo(shift);La fonction générique memoize se charge maintenant de tout. Il suffit de lui passer le nom de la fonction à mémoïser (sous la forme d'une chaîne de caractères) pour obtenir le résultat escompté.
Un petit avertissement ici : toutes fonctions ne se prêtent par à la mémoïsation. En particulier, on ne peut en principe mémoïser que des fonctions « pures », c'est-à-dire des fonctions dont la valeur de retour ne dépend que des arguments d'appel. Une fonction dont la valeur de retour dépendrait d'une variable globale ou de la date système ne peut probablement pas être mémoïsée, car elle risquerait de renvoyer des résultats faux. Et il ne sert à rien de mémoïser une fonction qui est déjà très rapide, par exemple parce qu'elle effectue un calcul simple : la version mémoïsée risque alors d'être plus lente.
L'objectif, dans cette section, était seulement de montrer comment peut marcher une fonction de mémoïsation calquée sur le fonctionnement de nos décorateurs. Il resterait beaucoup à faire pour qu'elle puisse traiter tous les cas de figure. Nous n'irons pas plus loin ici, parce que ce n'est pas l'objet principal de ce tutoriel et surtout parce qu'il existe un module standard (donc présent par défaut dans toute distribution ordinaire de Perl, vous n'avez rien à installer), Memoize, écrit par Mark-Jason Dominus, qui fait tout cela. C'est évidemment ce module que vous devriez utiliser si vous désirez mémoïser une fonction. Son utilisation est très simple :
use Memoize;
memoize('fonction_lente');
fonction_lente(arguments); # Plus rapide qu'avant (en principe)4-3. Autres utilisations des techniques employées ici▲
La technique consistant à écrire directement dans la table des symboles peut fournir une forme parfois utile de « sucre syntaxique ». La présente section 4.3 a été ajoutée dans cet article suite à la demande d'un lecteur désirant employer les techniques présentées ici sans avoir besoin à proprement parler d'un décorateur.
Considérons l'exemple d'une usine à fonctions qui crée dynamiquement des fermetures agissant comme des itérateurs. Prenons un cas très simple de deux itérateurs, respectivement sur des nombres pairs et impairs. Nous pouvons écrire l'usine à fonctions suivante :
sub cree_iter {
my $val = shift;
return sub { return $val += 2;}
}
my $iter_pair = cree_iter(0);
my $iter_impair = cree_iter(1);Appelons maintenant 5 fois l'itérateur de nombres pairs, 15 fois celui de nombres impairs et 5 fois celui des nombres pairs :
print $iter_pair->(), " " for 1..5; print "\n";
print $iter_impair->(), " " for 1..15; print "\n";
print $iter_pair->(), " " for 1..5; print "\n";À l'exécution, cela fonctionne parfaitement, nos itérateurs fonctionnent bien et indépendamment l'un de l'autre :
$ perl iter_pair_impair.pl
2 4 6 8 10
3 5 7 9 11 13 15 17 19 21 23 25 27 29 31
12 14 16 18 20Le seul problème est que la syntaxe :
print $iter_pair->();peut manquer quelque peu de convivialité pour un programmeur débutant. De plus, dans certaines entreprises, avoir une « fonction » dont le nom commence par le sigil $ est contraire aux normes de codage. Du coup, cette société ne pourra peut-être pas utiliser le beau module dans lequel nous avions logé ces itérateurs. Qu'à cela ne tienne. Il est possible dans un tel cas d'utiliser un peu de sucre syntaxique pour remédier à cette petite difficulté. Le code de notre module pourra contenir ce qui suit :
#!/usr/bin/perl
use warnings;
use strict;
sub cree_iter {
my $val = shift;
return sub { return $val += 2;}
}
*main::iter_pair = cree_iter(0);
*main::iter_impair = cree_iter(1);Et le code utilisateur sera maintenant plus simple et conforme aux normes de codage de l'entreprise :
print iter_pair(), " " for 1..5; print "\n";
print iter_impair(), " " for 1..15; print "\n";
print iter_pair(), " " for 1..5; print "\n";Ce qui affichera la même chose que précédemment.
Bien sûr, le nom des fonctions créées dans la table des symboles est ici codé en dur, ce qui manque singulièrement de souplesse d'utilisation. Mais nous pouvons facilement créer une fonction de création d'itérateurs bien plus générique, prenant en paramètre le nom de la fonction à créer, le pas d'incrémentation de l'itérateur et sa valeur initiale et implantant directement l'itérateur voulu dans la table des symboles :
sub cree_iter_quelconque {
my ($name, $multiple, $start_val) = @_;
no strict "refs";
*{"main::$name"} = sub { return $start_val += $multiple;}
}Maintenant, l'utilisateur de cette fonction peut créer lui-même ses propres itérateurs et les employer sans avoir à connaître le petit tour de magie blanche effectué dans la fonction :
cree_iter_quelconque("iter_pair", 2, 0);
cree_iter_quelconque("iter_impair", 2, 1);
cree_iter_quelconque("iter_triples", 3, 0);
print iter_pair(), " " for 1..5; print "\n";
print iter_impair(), " " for 1..15; print "\n";
print iter_triples(), " " for 1..5; print "\n";Ce qui imprime :
2 4 6 8 10
3 5 7 9 11 13 15 17 19 21 23 25 27 29 31
3 6 9 12 155. Lectures complémentaires▲
L'idée de départ de ce tutoriel m'est venue à la lecture de ce billet d'Ynon Perek : Fixing Legacy Perl Functions With Decorators.
Pour tout ce qui concerne les fonctions d'ordre supérieur, les coderefs, les fonctions anonymes, les fermetures, etc., je ne peux que conseiller la lecture de mon tutoriel en trois parties sur la programmation fonctionnelle en Perl, en particulier la Partie 2 : les fonctions d'ordre supérieur et la Partie 3 : étendre le langage.
L'excellent livre de Mark-Jason Dominus, Higher Order Perl (2005, Morgan Kauffman Publishers) couvre en détail beaucoup des points abordés ici, en particulier les fonctions d'ordre supérieur et la mémoïsation, et beaucoup d'autres choses passionnantes. Ce livre est disponible en téléchargement gratuit au format PDF sur le site de l'auteur (n'hésitez pas, allez voir), mais le sujet est suffisamment ardu pour que je recommande l'acquisition de la version papier. C'est en tous cas ce que j'ai fini par faire, je ne le regrette vraiment pas.
Le module Hook::LexWrap de Damian Conway permet d'ajouter des fonctions de prétraitement ou de post-traitement à une fonction donnée. Voir aussi le module Sub::Prepend de Johan Lodin, ainsi que Hook::PrePostCall de Philippe Verdret et Hook::WrapSub de John Porter. La documentation afférente à ce dernier module contient des liens vers d'autres modules faisant le même genre de choses.
Enfin, le lecteur pourra trouver des compléments intéressants sur les techniques avancées en Perl abordées ici dans les livres Advanced Perl Programming, 2nd ed. (2005), de Simon Cozens, et Mastering Perl (2014), de brian d foy, tous les deux publiés par O'Reilly Media.
6. Conclusion▲
Les décorateurs sont une technique qu'il est utile d'avoir dans sa boîte à outils. Nous avons présenté deux exemples typiques d'utilisation (ajouter des traces d'exécution à une fonction ou munir une fonction d'un cache permettant d'en accélérer le fonctionnement), mais il existe de nombreux autres cas où l'on désire modifier le comportement d'une fonction sans altérer son code. Les décorateurs peuvent notamment permettre d'éviter de la duplication de code ; même s'il existe des modules spécialisés le faisant très bien, on peut également se servir de décorateurs pour faire du benchmark (comparer les performances de différentes fonctions) ou pour profiler du code (mesurer le temps passé dans chaque fonction d'un programme).
Leur présentation nous a également permis de présenter quelques méthodes de programmation assez avancées en Perl qu'il est utile de connaître et d'utiliser occasionnellement, mais dont il ne faut pas non plus abuser. Ici, cela nous a permis d'étendre le langage, c'était à mon humble avis pleinement justifié.
7. Remerciements▲
Je remercie vivement Laurent Ott pour ses précieuses suggestions d'améliorations et de corrections, Djibril pour la relecture technique de ce texte et Claude Leloup pour la relecture orthographique. Merci également à Winjerome pour son assistance lors de la publication.
8. Annexe : le nombre d'or (ou divine proportion)▲
Supposons que l'on désire diviser un segment de droite AB en deux parties telles que le rapport de la plus grande CB à la petite AC soit égale au rapport du tout (AB) à la plus grande CB. On a donc : CB/AB = AC/CB. Ou, en renommant les segments, b/a = (a+b)/b.
A C B
----------/----------------
a | bEn posant a = 1, la longueur de b est trouvée par l'équation x = (x+1)/x, soit x2 - x - 1 = 0.
En résolvant l'équation, on trouve la racine positive suivante : x = b = b/a = (1 + √5)/2, soit 1,6180339887499... C'est ce que l'on appelle le nombre d'or (ou section dorée), souvent noté φ (phi). L'autre racine de l'équation est égale à - (1 - √5)/2 = -0,6180339887499..., et se trouve être aussi égale à -1/φ.
Ce rapport est considéré par beaucoup d'artistes comme celui représentant les proportions les plus harmonieuses. D'où le nom de divine proportion qui lui est parfois donné. L'architecte romain Vitruve, Luca Pacioli, Léonard de Vinci, Nicolas Poussin, Le Corbusier, Pablo Picasso et Paul Valéry figurent parmi les artistes qui lui attachaient beaucoup d'importance.
Ce nombre possède de nombreuses propriétés arithmétiques et géométriques remarquables.
Par exemple, φ possède les propriétés suivantes :
φ-1 = φ - 1, φ2 = φ + 1, φ3 = 2φ + 1, φ4 = 3 φ + 2 et φ5 = 5 φ + 3.
Ce qui se traduit numériquement comme suit :
- φ-1 = 0,6180339887 ;
- φ0 = 1 ;
- φ = 1,6180339887 ;
- φ2 = 2,6180339887 ;
- φ3 = 4,2360679775 ;
- φ4 = 6,8541019662 ;
De même, le nombre d'or φ satisfait également les relations suivantes :
(φ + 1) / φ = φ = 1 / (φ - 1).
En géométrie, prenons l'exemple d'un rectangle d'or, c'est-à-dire dont le rapport entre la longueur et la largeur est égale au nombre d'or. C'est le cas du rectangle ABCD dessiné en bleu ciel sur la figure ci-dessous : le rapport AD/AB est égal à φ.
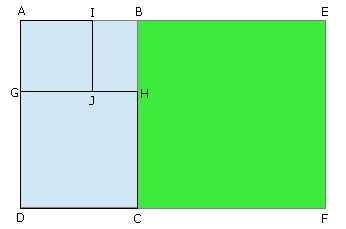
Si nous ajoutons le carré BCFE dont le côté est égal à la longueur du rectangle (en vert à droite), le nouveau grand rectangle formé AEFD est également un rectangle d'or.
Inversement, si nous retranchons un carré GHCD (en bas à gauche) du rectangle bleu ciel d'origine, le rectangle ABHG restant en haut à gauche est également un rectangle d'or. Puisque c'est un rectangle d'or, nous pouvons appliquer la même recette et retrancher à nouveau un carré AIJG (en haut à gauche) et obtenir un nouveau rectangle d'or (le petit rectangle IBHJ). Et nous pourrons bien sûr continuer ainsi autant que nous le désirons.
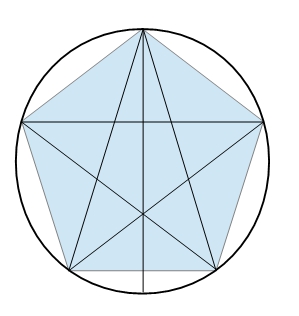
Toujours en géométrie, comme l'expression arithmétique du nombre d'or fait intervenir la racine carrée de cinq, on retrouve sans surprise le nombre d'or un peu partout dans les rapports de distance des pentagones réguliers (convexe et étoilé), ainsi que du décagone régulier. La figure ci-dessous contient pas moins de 25 triangles d'or et de 20 rapports dorés sur les différents segments de droite. Et le rapport d'homothétie entre le grand pentagone inscrit dans le cercle et le petit pentagone au centre est égal au carré du nombre d'or.
Notons enfin qu'il n'est guère surprenant de retrouver le nombre d'or dans le nombre d'appels de notre fonction fibo. Le nombre d'or est naturellement très présent dans la suite mathématique des nombres de Fibonacci. Le rapport entre deux nombres de Fibonacci consécutifs converge lui-même vers le nombre d'or (et le fait plus rapidement que notre formule des appels de la fonction fibo). Par exemple, le rapport entre le 25e nombre de Fibonacci et son prédécesseur est égal à : 75025 / 46368 = 1,6183398895, soit une approximation du nombre d'or (1,6183398875) avec les huit premières décimales correctes.
Il existe un autre lien entre la suite de Fibonacci et le nombre d'or. Vous vous souvenez sans doute de cette propriété des puissances de φ :
φ1 = φ, φ2 = φ + 1, φ3 = 2φ + 1, φ4 = 3 φ + 2, φ5 = 5 φ + 3, φ6 = 8 φ + 5...
Les deux coefficients de cette formule sont des nombres de Fibonacci consécutifs. En fait, on a :
kitxmlcodelatexdvp\varphi^{n} = fib_{n} \times \varphi + fib_{n-1}finkitxmlcodelatexdvpCurieux, non ?